TOC
This is learning note of The Seasoned Schemer, the code of my note is from here with edition:
pkrumins/the-seasoned-schemer: All the Scheme code examples from the book “The Seasoned Schemer”
This book is continuous to book The Little Schemer. The notes can be found in previous articles.
Chapter 11 Welcome Back to the Show
Firstly, we begin by defining function (two-in-a-row?) to test whether there are two
identical atoms in a row in a list. An initial trial is to use a function
(is-first?) that checks if the first and the second atom in the list are equal. If not, the (or) predicate will make sure the
function recursively checking the rest of list until there are two identical atoms appear.
(define is-first?
(lambda (a lat)
(cond
((null? lat) #f)
(else (eq? (car lat) a)))))
(define two-in-a-row?
(lambda (lat)
(cond
((null? lat) #f)
(else
(or (is-first? (car lat) (cdr lat))
(two-in-a-row? (cdr lat)))))))
(two-in-a-row? '(Italian sardines sardines spaghetti parsley)) ;-> trueThere are other ways to realize the same functionality. A slight issue of the above one
is that, it is the (or two-in-a-row?) get to decide termination.
For example cases
(two-in-a-row? '(a)) and (two-in-a-row? '(a b)) both print #f. For the first
case the function does not immediately terminate - even though the (is-first? a '()) returns #f, the (or two-in-a-row?) still gets called for at least another round. The same thing
happen in the latter example in the second round of (two-in-a-row?). That means the (or)
design is systematically less efficient - in this chapter, all we will learn is to make sure
the program as efficient as possible.
So we can rewrite (is-first?) to make it immediately terminate for empty lat, like this:
(define is-first-b?
(lambda (a lat)
(cond
((null? lat) #f)
(else (or (eq? (car lat) a)
(two-in-a-row-2? lat))))))
(define two-in-a-row-2?
(lambda (lat)
(cond
((null? lat) #f)
(else
(is-first-b? (car lat) (cdr lat))))))
;(two-in-a-row-2? '(Italian)) will terminate in the first predicate of is-first-b?Meanwhile we notice that the (is-first-b?) has a very similar procedure to
(two-in-a-row-2?). A small change can make (is-first-b?) very similar to its
master function - so calling two functions is almost like recursively calling one. The
core (is-first-b?) uses intermediate argument (a) to save the first element
for comparison, using (preceding) is identical to using (a).
;rewrite is-first-b?
(define two-in-a-row-b?
(lambda (preceding lat)
(cond
((null? lat) #f)
(else (or (eq? (car lat) preceding)
(two-in-a-row-b? (car lat) (cdr lat)))))))
(define two-in-a-row-final?
(lambda (lat)
(cond
((null? lat) #f)
(else (two-in-a-row-b? (car lat) (cdr lat))))))
;(two-in-a-row-final? '(Italian sardines sardines spaghetti parsley)) -> trueNotice: although they are similar, the (two-in-a-row-b?) has
two arguments whereas the (two-in-a-row-final?) only has one argument. In next chapter, we will see
how to use (letrec) to isolate the definition of (two-in-a-row-b?), so that
we can wrap and use it as a black box.
Another function stores step-by step sums of a tuple. It has similar procedure like the above, recursively operating the first and second atom of a list, with a changing intermediate argument saving the by-product for every step.
(define sum-of-prefixes-b
(lambda (sonssf tup) ; sonssf stands for 'sum of numbers seen so far'
(cond
((null? tup) '())
(else (cons (+ sonssf (car tup))
(sum-of-prefixes-b
(+ sonssf (car tup))
(cdr tup)))))))
; sum-of-prefixes function finds the running sum of a list of numbers
(define sum-of-prefixes
(lambda (tup)
(sum-of-prefixes-b 0 tup)))
;(sum-of-prefixes '(2 1 9 17 0)) -> '(2 3 12 29 29)And another case of selecting reversed items base on the number of the atom. So far, we have seen enough examples of the eleventh commandment: use additional arguments when a function needs to know what the other arguments to the function have been like so far.
(define scramble-b
(lambda (tup rev-pre)
(cond
((null? tup) '())
(else
(cons (pick (car tup) (cons (car tup) rev-pre))
(scramble-b (cdr tup)
(cons (car tup) rev-pre)))))))
(define scramble
(lambda (tup)
(scramble-b tup '())))
; Examples of scramble
(scramble '(1 1 1 3 4 2 1 1 9 2)) ; '(1 1 1 1 1 4 1 1 1 9)
(scramble '(1 2 3 4 5 6 7 8 9)) ; '(1 1 1 1 1 1 1 1 1)
(scramble '(1 2 3 1 2 3 4 1 8 2 10)) ; '(1 1 1 1 1 1 1 1 2 8 2)Chapter 12 Take Cover
In the last chapter we have seen again how to separately define and call recursive functions, with some designing improvement for efficiency. There is a natural thinking out of this: what if we combine them together? Actually we have seen combining functions with lambda expression and recursion in The Little Schemer, such as currying, Y combinator.
But there is an issue haven’t been mentioned: redundancy. Lots of similar parameters are called/updated with unnecessary amount of times, which are at expense of time, space or reading complexity. In next few chapters, we will see a few different ways designed to alleviate this issue.
The first way is to use (letrec) with lexical closure to wrap function
in function to make the outer function have clearer shape.
Let’s firstly review Y combinator:
;deducted in chapter 9 in The Little Schemer
(define Y
(lambda (le)
((lambda (f) (f f))
(lambda (f)
(le (lambda (x) ((f f) x)))))))
; An example of using Y-combinator to measure length and applied to '(a b c)
((Y (lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))) '(a b c)) ; produces output 3We can use Y combinator to rewrite (multirember) that removes multi-members from a list.
;old friend multirember
(define multirember
(lambda (a lat)
(cond
((null? lat) '())
((eq? (car lat) a)
(multirember a (cdr lat)))
(else
(cons (car lat) (multirember a (cdr lat)))))))
; No need to pass 'a' around in multirember
; Use Y-combinator not to pass it around
(define multirember
(lambda (a lat)
((Y (lambda (mr)
(lambda (lat)
(cond
((null? lat) '())
((eq? a (car lat)) (mr (cdr lat)))
(else
(cons (car lat) (mr (cdr lat))))))))
lat)))
(multirember 'a '(a b c a a a x)) ;-> '(b c x)We can see from the above that (multirember) has two arguments - a: the word we
want to remove; lat: the candidate list. a is contant all the time but
lat becomes shorter and shorter in every recursion. We re-write (multirember) in the second
definition by adding another layer to just pass the arguments. The major
difference is the execution for (eq? and else) predicates, the (mr) get
called without a as argument anymore.
What is the benefit of doing this? It separates the procedures of applying a
and lat, making the repetitive procedure (mr) easier for having less argument. You would probably wonder, instead of using Y combinator, what if I use currying learned from The
Little Schemer to write it, maybe like this?
(define mr
(lambda (lat)
(cond
((null? lat) '())
((eq? a (car lat)) (mr (cdr lat)))
(else
(cons (car lat) (mr (cdr lat)))))))
(define multirember
(lambda (a lat)
(mr lat)))When we apply it, we would notice problems, with step two result, instead of
finding (mr) function, the interpreter will firstly substitute a with ‘c and lat with '(c d), which will report error
because we did not specify a in (multirember). The third part is procedure we actually want.
;step 1
(multirember 'c '(c d))
;step 2
((lambda (a lat)
(mr lat)) 'c '(c d)) ;-> error variable 'a is not defined
;what we actually want it
((lambda (a lat)
((lambda (lat)
(cond
((null? lat) '())
((eq? a (car lat)) (mr (cdr lat)))
(else
(cons (car lat) (mr (cdr lat)))))))
lat))
'c '(c d))How do we organize code to achieve the function we want? The difference between the
right and wrong function is holding the argument substitution until after applying
the (mr) function. Apart from using layer by layer lambda functions, we can use (letrec) to define:
(define multirember-letrec
(lambda (a lat)
((letrec
((mr (lambda (lat)
(cond
((null? lat) '())
((eq? a (car lat)) (mr (cdr lat)))
(else
(cons (car lat) (mr (cdr lat))))))))
mr)
lat)))
(multirember-letrec 'apple '(apple bbb)) ;-> '(bbb)As the it says in the book, the implementation of (lambda (a lat)) is
equal to calling ((letrec ((mr..)) mr) lat). We can put the
above code in DrRacket see exactly how (letrec) part is called:

Here are more information about the concept of (letrec):
3.9 Local Binding: let, let*, letrec, …
Teach Yourself Scheme in Fixnum Days
We slightly adding a bit syntax sugar, changing the ((letrec ((mr..)) mr) lat) by moving the lat inside as
(letrec ((mr..)) (mr lat)):
(define multirember-letrec
(lambda (a lat)
(letrec
((mr (lambda (lat)
(cond
((null? lat) '())
((eq? a (car lat)) (mr (cdr lat)))
(else
(cons (car lat) (mr (cdr lat))))))))
(mr lat))))
(multirember-letrec 'apple '(apple bbb))By this function we successfully achieve the function we want without error as
above. With the syntax sugar, the function is very easy to read: we are just
using (letrec) to define a local recursive function that knows the definition
of a, which is called naming part. Then we implement the function to a list lat,
which is called valuing part.
Of course you could always use traditional, old friend one piece (multirember). The reason we have
to explore a correct way to call compound function to define it, is to isolate every part in
the future so that we could define more versatile functions.
That’s a naming with valuing procedure, this function can also be used to produce functions - if we isolate the predicate part with a function, we can procedure different types of functions. We have seen this in Y combinator section - we just add more layers.
(define multirember-f
(lambda (test?)
(lambda (a lat)
(cond
((null? lat) '())
((test? a (car lat)) ((multirember-f test? ) a (cdr lat)))
(else
(cons (car lat) ((multirember-f test?) a (cdr lat))))))))
;we can also use letrec
(define multirember-f
(lambda (test?)
(letrec
((m-f
(lambda (a lat)
(cond
((null? lat) '())
((test? a (car lat)) (m-f a (cdr lat)))
(else
(cons (car lat) (m-f a (cdr lat))))))))
m-f)))Notice that the function (lambda a lat) as a whole is inside the (letrec),
so the entire function (multirember-f) uses test? as argument and returns a function as result. The
returned function will referred as m-f. When substituting (test?) as (eq?)
we get our old friend (multirember). You might notice the (m-f) becomes
(mr) but they are basically the same thing. Parameter names don’t matter as
long as they are consistent.
(define multirember-eq? (multirember-f eq?)); multirember-eq? == multirember
(define multirember
(letrec
((mr
(lambda (a lat)
(cond
((null? lat) '())
((eq? a (car lat)) (mr a (cdr lat)))
(else
(cons (car lat) (mr a (cdr lat))))))))
mr))The involvement of (lambda (test?) layer enables us to design a function for
any function possibilities: with (test?) satisfied, we can call the procedure
(m-f) on something.
Let’s see another function: remember how we design (union) function to merge two sets: we traverse every element in set1, if it
is also a member in set2, we skip; otherwise we cons this element to set2:
(define union
(lambda (set1 set2)
(cond
((null? set1) set2)
((member? (car set1) set2) ;<- notice the order of arguments
(union (cdr set1) set2))
(else
(cons (car set1) (union (cdr set1) set2))))))
;we can of course define with letrec
(define union-letrec
(lambda (set1 set2)
(letrec
((U (lambda (set)
(cond
((null? set) set2)
((member? (car set) set2) ;<- notice the order of arguments
(U (cdr set)))
(else
(cons (car set) (U (cdr set))))))))
(U set1))))
(union-letrec
'(tomatoes and macaroni casserole)
'(macaroni and cheese))Now set2 is the unchanged parameter in function, set1 is getting shorter and
shorter in recursion. Similar with (multirember-letrec), the procedure firstly
passes the unchanged set2, making the (U) function only has one changing
parameter (set) which then got substituted by traversed set1.
It seems using the extra step for separation is not a big deal, especially when in the (multirember-letrec)
example where a and lat are so distinctive that we would not make mistake in
applying them. But from (union-letrec) we will see things particularly need
to me mindful. The only difference between the below functions are the order of
the parameters:
;right for the above union-letrec function
(define member?-1
(lambda (a lat)
(cond
((null? lat) #f)
((eq? (car lat) a) #t)
(else (member? a (cdr lat))))))
;wrong for the above union-letrec function, (but correct as itself).
(define member?-2
(lambda (lat a)
(cond
((null? lat) #f)
((eq? (car lat) a) #t)
(else (member? (cdr lat) a)))))If the (member) function (defined outside the (union-letrec)) have stated to take the first element as list to
traverse, when writing (union-letrec) we have to make sure the arguments passed
to (member?) has the consistent order.
Meanwhile, we can just define the (member?) inside (union-letrec) since
(letrec) allows us to define multiple functions at the same time.
(define union-letrec-protected
(lambda (set1 set2)
(letrec
((U (lambda (set)
(cond
((null? set) set2)
((M? (car set) set2)
(U (cdr set)))
(else
(cons (car set) (U (cdr set)))))))
(M?
(lambda (a lat)
(cond
((null? lat) #f)
((eq? (car lat) a) #t)
(else
(M? a (cdr lat)))))))
(U set1))))
(union-letrec-protected
'(tomatoes and macaroni casserole)
'(macaroni and cheese)) ; '(tomatoes and macaroni casserole cheese)Currently it has the form of (letrec (U M) (U set1)), where the (U) and (M?) are in
the same lay. This design only isolates the unchanged variable set2. But we
notice that there is also an unchanged variable a so we should wrap (M?) in
a inner layer of the function (U):
(define union-letrec-protected-12
(lambda (set1 set2)
(letrec
((U (lambda (set)
(cond
((null? set) set2)
((M? (car set) set2)
(U (cdr set)))
(else
(cons (car set) (U (cdr set)))))))
(M?
(lambda (a lat)
(letrec
((N? (lambda (lat)
(cond
((null? lat) #f)
((eq? (car lat) a) #t)
(else
(N? (cdr lat)))))))
(N? lat)))))
(U set1))))Another example we’ve seem is (two-in-a-row), let’s try rewrite it with (letrec)
too. Last time our final definition is: defining recursive function (two-in-a-row-b?) first, then
call it in (two-in-a-row-final?). At here, the separation of two function is
no longer for distinguishing changing and unchanged variables, but to separate
procedures as black box to for future purpose.
(define two-in-a-row-b?
(lambda (preceding lat)
(cond
((null? lat) #f)
(else (or (eq? (car lat) preceding)
(two-in-a-row-b? (car lat) (cdr lat)))))))
(define two-in-a-row-final?
(lambda (lat)
(cond
((null? lat) #f)
(else (two-in-a-row-b? (car lat) (cdr lat))))))
;---define above function with letrec
(define two-in-a-row?
(lambda (lat)
(letrec
((W (lambda (a lat)
(cond
((null? lat) #f)
((eq? a (car lat)) #t)
(else
(W (car lat) (cdr lat)))))))
(cond
((null? lat) #f)
(else (W (car lat) (cdr lat)))))))
;here is another version
(define two-in-a-row-2?
(letrec
((W (lambda (a lat)
(cond
((null? lat) #f)
((eq? a (car lat)) #t)
(else
(W (car lat) (cdr lat)))))))
(lambda (lat)
(cond
((null? lat) #f)
(else (W (car lat) (cdr lat)))))))
; Test two-in-a-row-2?
(two-in-a-row-2? '(Italian sardines spaghetti parsley))And (sum-of-prefixes) can be rewrite like this:
(define sum-of-prefixes
(lambda (tup)
(letrec
((S (lambda (sss tup)
(cond
((null? tup) '())
(else
(cons (+ sss (car tup))
(S (+ sss (car tup)) (cdr tup))))))))
(S 0 tup))))
(sum-of-prefixes '(2 1 9 17 0)) ; '(2 3 12 29 29)The applying procedures for the first steps are:

Chapter 13 Hop, Skip, and Jump
We are continuing the story of (letrec). In the last part of chapter 12, from the application of
(two-in-a-row letrec) and (two-in-a-row-2) we have seen that the letrec
function can be defined and called anywhere in any function. The purpose is no
longer limited to “separating changing and unchanged” variables. It is true that
the letrec closure can be used anywhere in function for any relevant needs.
Let’s see more examples.
We were told that set is a list
consists of non-repeated atoms. Remember we defined two functions for sets:
(intersect set1 set2) that returns the common atoms of two input sets; and
(intersectall) that use (intersect) to find common atoms of list of sets. Let’s first rewrite (intersect) with (letrec), which is simple:
(define intersect
(lambda (set1 set2)
(cond
((null? set1) '()) ; don't forget the 1st commandment
((member? (car set1) set2)
(cons (car set1) (intersect (cdr set1) set2)))
(else
(intersect (cdr set1) set2)))))
(intersect '(a b x c d) '(q w e x r t y a)) ;-> '(a x)
(define intersect-letrec
(lambda (set1 set2)
(letrec
((I (lambda (set)
(cond
((null? set) '())
((member? (car set) set2)
(cons (car set) (I (cdr set))))
(else
(I (cdr set)))))))
(I set1))))
(intersect-letrec '(a b x c d) '(q w e x r t y a)) ;-> '(a x)This is old friend (intersectall):
(define intersectall
(lambda (lset)
(cond
((null? (cdr lset)) (car lset)) ; don't forget the 1st commandment
(else
(intersect (car lset)
(intersectall (cdr lset)))))))
(intersectall '((a) (a) (a))) ;-> '(a)The old friend (intersectall) works like this: the input can be classified to
possibilities that: list containing zero set, one set or more than one sets. In
the Little Schemer we assumed the input is not null so last time we only prepared
function for list with one or more sets. We can fix
the condition ignored by us at the last time: adding another line of predicate
for pure null input:
(define intersectall
(lambda (lset)
(cond
((null? lset) '()) ;<- so far the only difference is here
((null? (cdr lset)) (car lset))
(else
(intersect (car lset)
(intersectall (cdr lset)))))))Here is the letrec function of (intersectall). As we have stressed in last chapter, the outer lambda
expression’s parameter use name lset, which is the same with the inner lambda
expression’s parameter name
lset. This is a coincidence, and parameter in A can use any name as a
name holder, which will be substituted by the lset of (else (A lset)).
(define intersectall-letrec
(lambda (lset)
(letrec
((A (lambda (lset) ;<-there is one more pair of parenthesis for more function
(cond
((null? (cdr lset)) (car lset))
(else
(intersect (car lset)
(A (cdr lset))))))))
(cond
((null? lset) '())
(else (A lset))))))
(intersectall-letrec '((a b c d) (b c d e) (c d e f))) ; '(c d)The (null? lset) works as terminating condition as stated by the first commandment,
which will be use every time in the inner recursion, and only checks once at the
very beginning. We wrap the remaining old friend in (A) and call it.
However there is still an inefficiency issue: the
terminating condition appears too late. The terminating condition is hidden in A
, and it won’t be triggered until the (cdr lat) become null.
For example:
(intersectall-letrec '((a b c d) () (c d e f)))We do not need to run function to realize that the
intersection is null. But in DrRacket if we use stepper we can set it takes 73
steps for the function to finish: the input list is peeled layer by layer, until
the function (null? (cdr lset) in (A) receives the LAST set '(c d e f),
and it has to finish computing all the remembered value (intersect (intersect (intersect..))).
So it would be more efficient if we can add a predicate
inside, testing null (car lset) to terminate immediately. That’s where we need (letcc):
;we prefer this version than the below one
(define intersectall
(lambda (lset)
(letcc hop ;<- add new function here
(letrec
((A (lambda (lset)
(cond
((null? (car lset)) (hop '())) ;<- add a predicate here
((null? (cdr lset)) (car lset))
(else
(intersect (car lset)
(A (cdr lset))))))))
(cond
((null? lset) '())
(else (A lset)))))))
;or another way to write, raised by Alonzo Church
(define intersectall-letcc
(lambda (lset)
(call-with-current-continuation ;<- add a name here
(lambda (hop) ;<- add new function here
(letrec
((A (lambda (lset)
(cond
((null? (car lset)) (hop '())) ;<- add a predicate here
((null? (cdr lset)) (car lset))
(else
(intersect (car lset)
(A (cdr lset))))))))
(cond
((null? lset) '())
(else (A lset))))))))
(intersectall-letcc '((a b c d) ( ) (c d e f)))We notice that in the first code block, two lines of code are added. When
finding (null? (car lset)) is true, we will call hop function making A hop
to the right position. The example helps to learn how the hop works. First the
input list will substitute the outer lat and the function starts to run,
triggering (A lset). The first round of loop wouldn’t trigger (hop) because
(car lset) is (3 mangos and) not null. But the second loop will trigger the
(hop) because (car (() (c d e f)) is true. The (hop) basically halts the
whole function and return ('()) for this case, regardless we have remembered (intersect (a b c d) something) to run. We only need to find the results of (letcc hop M), which in this case is (letcc hop (quote ()))).
Long story short, so far we design a function that would stop the first moment it detects a null set in list.
So (letcc) can be used to return value abruptly and promptly.
We are continuing improve the functions, because we notice something inefficient
again. We know the (intersectall) takes intersection of all sets in a list, by
(intersect) two sets once in turn. That means any two cases has no intersection
should make the whole process return null immediately.
(intersectall-letcc '((a b c d) (d e) (x y z)))For above example we need to take intersection between the third and
second, then with the first. Ideally a function should instantaneously stop when
finding the intersection for (x y z) and (d e) is (). But our current program won’t
tell until after running (intersect) several times. A feasible (not the best)
improvement is to fix (intersect):
(define intersect-letrec
(lambda (set1 set2)
(letrec
((I (lambda (set)
(cond
((null? set) '())
((member? (car set) set2)
(cons (car set) (I (cdr set))))
(else
(I (cdr set)))))))
(cond ;<- new line
((null? set2) (quote ())) ;<- new line
(else (I set1)))))) ;<- new lineWe say the above is not the best because, it only creates the best
efficiency for (intersect), not for (intersectall) yet. The ideal scenario
should be once there is a empty set in list, the (intersectall) should
immediately cease and return null list. In another word, we want
hop happening not only in one-out-of-two checking, but also in one-out-of-n
checking. Writing function like the below one would solve it. I suggest to
put the code in DrRacket to see the structure with better highlighting.
(define intersectall-ap
(lambda (lset)
(letcc hop
(letrec
((A (lambda (lset) ;<-intersectall
(cond
((null? (car lset)) (hop '()))
((null? (cdr lset)) (car lset))
(else
(I (car lset)
(A (cdr lset)))))))
(I (lambda (s1 s2) ;<-intersect
(letrec
((J (lambda (s1)
(cond
((null? s1) '())
((member? (car s1) s2)
(cons (car s1) (J (cdr s1))))
(else
(J (cdr s1)))))))
(cond
((null? s2) (hop '())) ;<-we can hop in minor function
(else (J s1)))))))
(cond
((null? lset) '())
(else (A lset))))))))
(intersectall-ap '((a b c d) (b c d e) (c d e f))) ;-> '(c d)Here is how the two functions have evolved to (intersectall-ap):
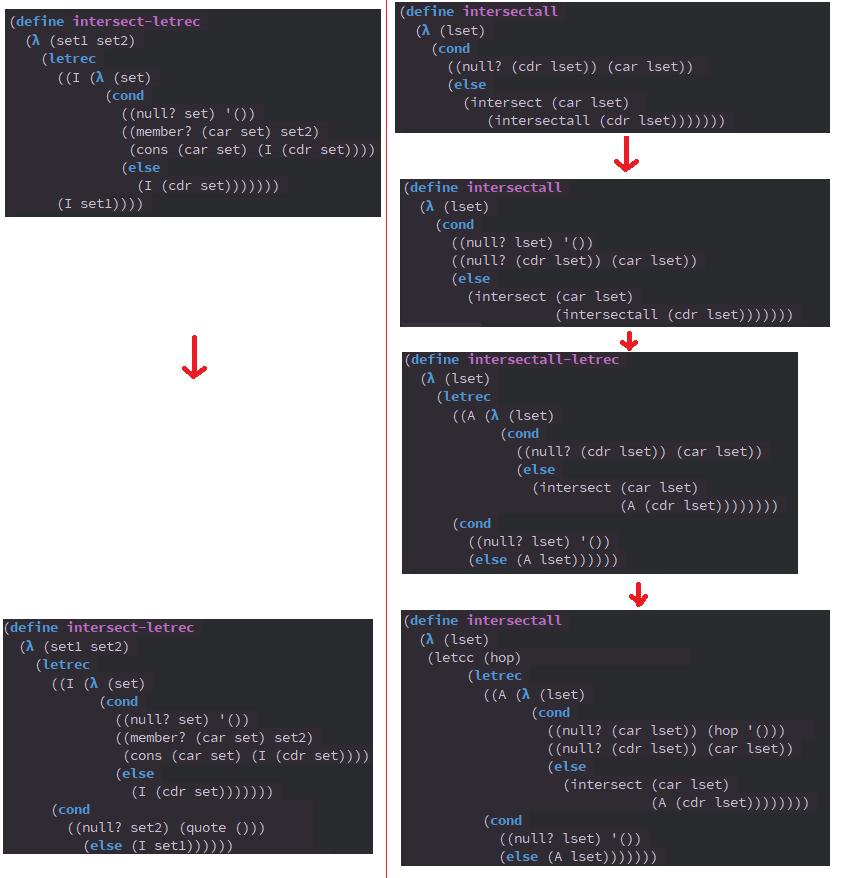
We have been familiar with more flexible application of (hop). Let’s see
another example. Firstly we rewrite old friend (rember) with letrec:
(define rember
(lambda (a lat)
(letrec
((R (lambda (lat)
(cond
((null? lat) '())
((eq? (car lat) a) (cdr lat))
(else
(cons (car lat) (R (cdr lat))))))))
(R lat))))The rember-beyond-first function (rember) everything beyond first match:
(define rember-beyond-first
(lambda (a lat)
(letrec
((R (lambda (lat)
(cond
((null? lat) '())
((eq? (car lat) a) '())
(else
(cons (car lat) (R (cdr lat))))))))
(R lat))))
(rember-beyond-first
'roots
'(noodles spaghetti spatzle bean-thread roots potatoes yam others rice))
;-> '(noodles spaghetti spaghetti bean-thread)The above function seems easy. It’s hard if we want a function that retains everything
AFTER a in a list. Luckily we have (skip) that helps us to realize it by
tweaking (rember-beyond-first) a little:
(define rember-upto-last
(lambda (a lat)
(letcc skip
(letrec
((R (lambda (lat)
(cond
((null? lat) '())
((eq? (car lat) a) (skip (R (cdr lat))))
(else
(cons (car lat) (R (cdr lat))))))))
(R lat))))))
(rember-upto-last
'roots
'(noodles spaghetti spatzle bean-thread roots potatoes yam others rice))
;-> '(potatoes yam others rice)The function works similar to (hop): when the function not triggered, we just
ignore it and run as usual. In the above example, it conses (noodles spaghetti spatzle bean-thread) until (roots) is input. The (skip (R (cdr lat)) means
we can eliminate all the pending conses and determine the value of (letcc skip (R (cdr lat))) where lat is (roots potatoes yam others rice). The remaining
list doesn’t contain roots, therefore it will be traversed and returns (roots potatoes yam others rice).
chapter 14
So far you must have realized, in addition to using (letrec letcc) and (hop skip) to terminate program, we also leanred an important concept in
programming: checking judgement and abormality processing. This is the major
concept in all programming: how can we design and improve a function which
considers all possible conditions while gurantees the efficiency at the same
time?
There is no one-for-all instruction for perfect program, but we can gain more and more insights by seeing improving an examples.
There is old friend (left most):
(define leftmost
(lambda (l)
(cond
((atom? (car l)) (car l))
(else (leftmost (car l))))))
(leftmost '(((a) b) (c d))) ;-> 'aBut it won’t work for input like ((()) a b) because we didn’t prepate for the
null input case. In addtion, we also want it to skip the null and return
meaningful atom. Let’s improve it:
(define leftmost-fixed
(lambda (l)
(cond
((null? l) '())
((atom? (car l)) (car l))
(else
(cond
((atom? (leftmost-fixed (car l)))
(leftmost-fixed (car l)))
(else (leftmost-fixed (cdr l))))))))
(leftmost-fixed '(((() x) ()))) ;-> 'xWe rewrite this by introducing (let) who helps define local function within functions.
(define leftmost-let
(lambda (l)
(cond
((null? l) '())
((atom? (car l)) (car l))
(else
(let ((a (leftmost-let (car l))))
(cond
((atom? a) a)
(else (leftmost-let (cdr l)))))))))
(leftmost-let '(((y) b) (c d))) ;-> 'ySimilarly, we define an improved version of (rember a lat) that removes the leftmost occurrence of a in lat.
(define rember1*
(lambda (a l)
(cond
((null? l) '())
((atom? (car l))
(cond
((eq? (car l) a) (cdr l))
(else
(cons (car l) (rember1* a (cdr l))))))
(else
(cond
((equal? (rember1* a (car l)) (car l)) ; if the list with 'a' removed doesn't change
(cons (car l) (rember1* a (cdr l)))) ; then recurse
(else
(cons (rember1* a (car l)) (cdr l)))))))) ; otherwise remove 'a'
(rember1*
'salad
'((Swedish rye) (French (mustard salad turkey)) salad))
;-> '((Swedish rye) (French (mustard turkey)) salad)comments powered by Disqus