TOC
Part one: The Little Schemer speedy referring note (1/3)-Katherine He Blog|何琪的博客 Part two: The Little Schemer speedy referring note (2/3)-Katherine He Blog|何琪的博客 Part three: The Little Schemer speedy referring note (3/3)-Katherine He Blog|何琪的博客
This is a quick reference note that I pull from the book The Little Schemer. The code in this note is from here with edition:
the-little-schemer/02-do-it-again.ss at master · pkrumins/the-little-schemer
The former chapters can be easily understood from reading the code without
counting parenthesis. However from this chapter, it is highly recommended to
download Drracket and use a stepper to run all the recurions. For example, the
stepper make the answer of soegaard very straightforward:
scheme - Y combinator discussion in “The Little Schemer” - Stack Overflow
This chapter introduces the idea of Y combinator based on recursion. We’ve seen that recursion is a function calling itself during defining itself, but when the function is just an lambda expression without name, what do we do?
The Y combinator provides a solution by designing an high order function, which is a function that takes a function as an argument and returns a function. Taking factorial as an example, we deduce a function G where G(factorial)=factorial. Let’s learn how to deduce step by step.
Chapter 9 and Again and Again and Again
The key of writing recursion is making sure there is termination condition.
That’s the basic requirement for function in both computation and mathmatics
area: a function is a mapping procedure which takes in an argument and produces
an output accordingly. We need to aviod any algorithm leading to infinite loop.
Here is an example of failed design: the (keep-looking) calls (pick) to see if a is equal to the random atom in lat (assuming the numbers in lat is random).
;pick return n-th element in lat:
(define pick
(lambda (n lat)
(cond
((zero? (sub1 n)) (car lat))
(else
(pick (sub1 n) (cdr lat))))))
(define keep-looking
(lambda (a sorn lat)
(cond
((number? sorn)
(keep-looking a (pick sorn lat) lat))
(else (eq? sorn a )))))
(define looking
(lambda (a lat)
(keep-looking a (pick 1 lat) lat)))
; Example of looking
(looking 'caviar '(6 2 4 caviar 5 7 3)) ; #t
(looking 'caviar '(6 2 grits caviar 5 7 3)) ; #fIn the first test case we can find that, the 'caviar is the 4th element in the
first example, and the list contains 4. So running it is very likely to hit the
termination condition. But in second example the 'caviar is the 4th element whereas no 4
is contained in the list, so the recursion will run forever, meaning the
function won’t always return a value for an input. This illed function is called
partial function as opposed to total function defined previously.
Let’s see another example. We’ve defined pair is a list containing two
s-expressions (s-expression: a binary tree). The shift takes a pair whose first component is a pair and builds a pair by shifting the second part of the first component into
the second component.
(define first
(lambda (p)
(car p)))
(define second
(lambda (p)
(car (cdr p))))
(define build
(lambda (s1 s2)
(cons s1 (cons s2 '()))))
;(shift '((a b) c)) -> '(a (b c))
;(shift '((a b) (c d))) -> '(a (b (c d)))
(define shift
(lambda (pair)
(build (first (first pair))
(build (second (first pair))
(second pair)))))
(define a-pair?
(lambda (x)
(cond
((atom? x) #f)
((null? x) #f)
((null? (cdr x)) #f)
((null? (cdr (cdr x))) #t)
(else #f))))
(define align
(lambda (pora)
(cond
((atom? pora) pora)
((a-pair? (first pora))
(align (shift pora))) ;******alarming
(else (build (first pora)
(align (second pora)))))))Based on (shift) we further creat (align). Don’t rush to run the function. Remember the seventh commandment emphasizes “recursion should happen on the subparts that are of the same nature:
either on the sublists of a list; or on the subexpressions of an arithmetic
expression”. We notice something alarming in the starred line in (align):
the (align) as well as (keep-looking) both creat new argument in recursion
that is not part of the original argument. It’s an indicator of ill, but
(align) will still generate output for every input, so it’s not partial function.
We will continue and define a very similar function (shuffle) below, which is partial. It won’t
produce value for some cases, since the a-pair predicate will always swap the items of pair, which
makes any input with form of ((a b) (c d)) trapped in infinite item swapping loop.
;(revpair '((a b) (c d))) -> ((c d) (a b))
(define revpair
(lambda (p)
(build (second p) (first p))))
(define shuffle
(lambda (pora)
(cond
((atom? pora) pora)
((a-pair? (first pora))
(shuffle (revpair pora)))
(else
(build (first pora)
(shuffle (second pora)))))))
(shuffle '(a (b c))) ; '(a (b c))
(shuffle '(a b)) ; '(a b)
(shuffle '((a b) (c d))) ; infinite swap pora Ctrl + c to break and input q to exitWe just define two different
ways to measure the mass of the first component of (align). The (length*) measures every
atom with same weight, whereas the (weight*) puts twice as much weight to the first component.
(define length*
(lambda (pora)
(cond
((atom? pora) 1)
(else
(+ (length* (first pora))
(length* (second pora)))))))
;(length* '((a b) c)) -> 3
;(length* '(a (b c)) -> 3
(define weight*
(lambda (pora)
(cond
((atom? pora) 1)
(else
(+ (* (weight* (first pora)) 2)
(weight* (second pora)))))))
;(weight* '((a b) c)) -> 7
;(weight* '(a (b c)) -> 5From (align) and (shuffle), we realize that whether the arguments will
decrease in recursion is not the key to infer whether a function is total. We
start to think if possible to develop a diagnose function to detect the partial
function. Let’s imaging making
up a function (will-stop?) without getting into detail. We want it to return
#t if the function would eventually terminate with returning value, and return #f it does not
stop. And itself has to be a total function, in which case (will-stop? will-stop>) has
to return #t.
What would happen if the input are (length) and (eternity) like these? Sounds cool: the (length) stops when the input is '(), so the (will-stop?) returns #t, great!
Meanwhile the (eternity) is partial and won’t stop for any input, which makes the
(will-stop?) returns #f whatsoever.
(define eternity
(lambda (x)
(eternity x)))
(define will-stop?
(lambda (x)
(eternity x)))
(define length
(lambda (lat)
(cond
((null? lat) 0)
(else (add1 (length (cdr lat)))))
(define will-stop?
(lambda (x)
(length x)))But you might also sense logical flaws already: if there is a function can make
(will-stop?) return #t
but won’t stop, the partial function detection function may eventually NOT
exist. If you cannot, the author has carefully come up with an example to show
why.
Let’s see this example:
(define last-try
(lambda (x)
(and (will-stop? last-try)
(eternity x))))In order to test if ths is a right function, we input () and that requires
evaluate (will-stop? last-try). Provided it returns #f (aka the last-try will
not stop with null input), then the whole function will stop and return #f.
Clearly this mother function (last-try (quote())) stops for null input, which
goes against the aka part in parenthesis. So we try the opposite hypothesis: it
returns #t (aka the last-try will stop with null input), and then we get to
evaluate (eternity (quote())), which never stops. And this time, it logically
goes against the hypothesis again. This makes the (will-stop?) a
function we can describe but can not define. The example delicately demonstrates
this by constructing a function
based on (will-stop?) which (will-stop?) cannot judge.
You might ask what if we just ban the logical contradiction part,
such as “preventing tested function from directly or indirectly calling (will-stop?)”.
In that case, will (will-stop?) exist? I am not sure. But that “using
functions without recursively calling itself” is exactly what we want to do
with the Y combinator.
A function calling itself directly or indirectly, is recursion. A nature wonder about recursion is that, if we want to call a function that haven’t been fully defined, how could we do it?
There are many ways to write programs to realize the same procedure. But a specific interpreter has clear rule to implement a function. In this chapter, we can use transformations and derivations to gain fundamental understanding of nested functions, to peel off the syntax sugar so that we can reform them to design elegant form.
We probably can re-write a recursive function to non-recursive one, then we can use it as much as we want. That’s what the Y combinator is for.
Let’s begin with recursive function we have seen, to see what part we can get
rid of and reform. We still use (length) as an example. Currently it is a fully defined function
recursive function. The input is a list and the output is a value (i.e. the
length of a list). It can use recursion inside itself because it has formal function name length.
;you have use to other name in DrRacket, coz length has been a build-in function
(define length
(lambda (l)
(cond
((null? l) 0)
(else
(add1 (length (cdr l)))))))
(length '(a b)) ;-> 2I highlight four key procedures to show how it adapts:

The thing about the recursion (length) is, it may look like the (length) is
calling itself. More broadly speaking, it is just calling a function happens to have the same
name with itself. The function will be used when the input (cdr l) is not null. It can be any
functions, so you
can try substituting (length) with any function you like. This equals to
having another layer of lambda expression to the function of (length):
(lambda (length)
(lambda (l)
(cond ((null? l) 0)
(else (+ 1 (length (cdr l)))))))Notice, you can try inputting any function in outer layer but most
functions will not work with non-null input list. For
example let’s call (eternity) instead of (length): when the list has more
than zero atom, the null predicate returns #f and (eternity '()) will be called and the function will trap in infinite loop.
;((lambda (length) ..) eternity)
;length<=0
(lambda (l)
(cond
((null? l) 0)
(else
(add1 (eternity (cdr l))))))It can still measure null list only in the applicative order interpreting, where the arguments will be instantaneously evaluated the leftmost innermost reducible expression before the function is applied.
But there is still a way to measure list with less
than one element. We just have to call length
measuring function on top of (length0) one more time.
;length<=1
(lambda (l)
(cond
((null? l) 0)
(else
(add1 (length0 (cdr l))))))
;length<=1
(lambda (l) ;read more details below if you don't understand here
(cond
((null? l) 0)
(else
(add1
((lambda(l)
(cond
((null? l) 0)
(else
(add1 (eternity (cdr l))))))
(cdr l))))))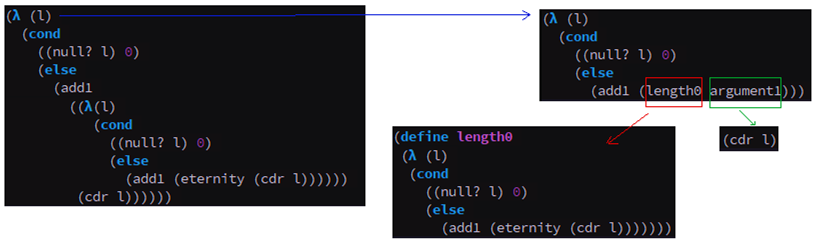
Recursively we can develop (length<=2) below. Can you explain why these
three functions are identical?
;length<=2
(lambda (l)
(cond
((null? l) 0)
(else
(add1 (length1 (cdr l))))))
(lambda (l)
(cond
((null? l) 0)
(else
(add1
((lambda(l)
(cond
((null? l) 0)
(else
(add1 (length0 (cdr l))))))
(cdr l))))))
(lambda (l)
(cond
((null? l) 0)
(else
(add1
((lambda(l)
(cond
((null? l) 0)
(else
(add1
((lambda(l)
(cond
((null? l) 0)
(else
(add1 (eternity (cdr l))))))
(cdr l))))))
(cdr l))))))
;let's give distinguished names to arguments in every layer
(lambda (l2) ;assume l2 = '(b c)
(cond
((null? l2) 0)
(else
(add1
((lambda(l1) ;then l1 <- cdr(l2) = '(c)
(cond
((null? l1) 0)
(else
(add1
((lambda(l0) ;then l0 <- cdr(l1) = '( )
(cond
((null? l0) 0) ;so here returns 0, and terminates
(else
(add1 (eternity (cdr l0))))))
(cdr l1))))))
(cdr l2))))))As you might imagine, the above form is not quite complete, so we were only saying
its got a “hidden layer of parameter”. Let’s make it slightly more formal by
separating (eternity) and calling it as argument. In the (length<=1) code we just want to use distinctive names for
you to see this procedure clearer.
;length<=0
((lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
eternity)
;length<=1
((lambda (f)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (f (cdr l)))))))
((lambda (g)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (g (cdr l)))))))
eternity))
;length<=2
((lambda (length)
(lambda(l)
(cond)
((null? l) 0)
(else (add1 (length (cdr l)))))))
((lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
((lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
eternity)))It’s absolutely normal to get confused when there are more layers of lambda expressions involved in a function/recursion. It helps to think whether the lambda expressions is being merely defined or being defined and called, i.e. counting the parenthesis very carefully. The difference between defining and calling is that calling a function has arguments involved:
;defining
(lambda (f)
(lambda (g)...)
)
;calling(f) with defining(g)
((lambda (f)
(lambda (g)...))
arguments-for-f)A more general case of calling with defining in lambda expression is called the
omega combinator. It has shape in the below picture and more information can be
found at Lambda calculus - Wikipedia
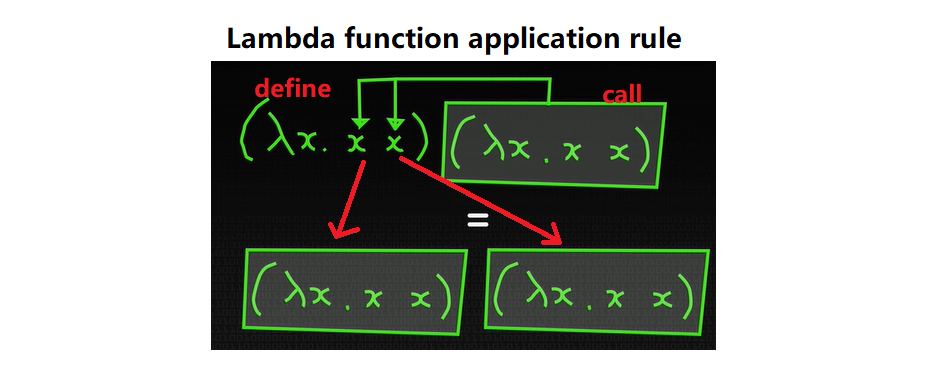
The above functions show repetitive content: the (length) part is being
called over and over, working on a shorter and shorter argument. Normally, we would write and save as a named
function for calling in the future like (define length). But, if we don’t
save it, instead we want to directly address it within other function, or even
address itself. How do we do that?
You may have realized the motivation of this question, addressing itself withing itself is exactly the nature of recursion. In this chapter we just want to find a good way to do it for anonymous functions.
If we can define length abstractly, we can call it to simplify the reptitive procedure.
This need is particularly necessary when there is going to be many algorithms
having similar repetitions as (length<=n).
Ok, we are finally reaching the core reforming step. We are giving the
formal calling form as equivalent to (define length):
(define length
(lambda (l)
(cond
((null? l) 0)
(else
(add1 (length (cdr l)))))))
(length '( )) ;-> 0
(length '(a b)) ;-> 2
;--------------------------------------------
((lambda (mk-length)
(mk-length eternity))
(lambda (length)
(lambda(l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))))
((mk-length eternity) '());-> 0
((mk-length eternity) '(a));-> errorFrom the above we can see instead of being a name defined by define, length can also work as an parameter/argument.
However there is a major difference: (define length) has only one lambda expression, the input must be
a list and the output is value. But the anonymous definition is adding another layer of lambda expression, the input and
output for the outer lambda expression (i.e. the whole function) will have
to be functions. It’s the output “function (λ l)” that will return value like
the defined length function.
Another very important note is that, the (define length) function
can evalue list with any length. the anonymous function can only evaluate input of null list, why? Because the input for
length must be function ((cdr l) sure won’t fit), so if we don’t want get error message, it will have to
terminate at (null? l) stage. Like we said, we will have to use call function more times if
we want to measure longer lists:
;length<=1
((lambda (mk-length)
(mk-length
(mk-length eternity)))
(lambda (length)
(lambda(l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))))
;length<=2
((lambda (mk-length)
(mk-length
(mk-length
(mk-length eternity))))
(lambda (length)
(lambda(l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))))In the (length<=0) function the only working part is ((null? l) 0) and the (else) predicate
would never got triggered. So in that predicate it doesn’t really matter whether
we call function (eternity), or itself (mk-length). We just change (eternity) to (mk-length):
; length<=0
((lambda (mk-length)
(mk-length mk-length)) ;<- we change here
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else
(add1 (length (cdr l))))))))The above code is still ONLY able to measure null list, because for other input,
it will have to expand (add1 (length (cdr l))) where the input of argument
has to be a function, defined by the (lambda (mk-length)(mk-length mk-length). But the input (cdr l) is a list. See how it fails in stepper:

As you might guess, we can just pass a random/any function to make it
successfully measure the length one list, since it will stop in (null? list) in the second
loop. For example any of these three functions could work:
((lambda (mk-length)
(mk-length mk-length))
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else
(add1 ((length add1) (cdr l))))))))
((lambda (mk-length)
(mk-length mk-length))
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else
(add1 ((length eternity) (cdr l))))))))
;This one is fundamentally different from the above two, why?
((lambda (mk-length)
(mk-length mk-length))
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else
(add1 ((length length) (cdr l))))))))The former two functions can only help you measure length one list. For
length two input it would fail in the function expansion, resulting in non-legitimate functions (add1 add1)
(eternity eternity) in the second loop. However, the third one won’t fail
because (length length) is a legitimate function, it can help us measure list
with any length. So functionally speaking, these two are finally consistent:
(define length
(lambda (l)
(cond
((null? l) 0)
(else
(add1 (length (cdr l)))))))
((lambda (mk-length)
(mk-length mk-length))
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else
(add1 ((length length) (cdr l))))))))All left job is just to make things extremely pithy. Let’s adding some syntax sugar here: since it doesn’t matter what we name the inner arguments, because it’s just an pseudo name inside a function. So we can name it anything as long as we keep naming and calling consistent. The last function above can be written as:
((lambda (mk-length)
(mk-length mk-length))
(lambda (mk-length)
(lambda (l)
(cond
((null? l) 0)
(else
(add1 ((mk-length mk-length) (cdr l))))))))The exercise in page 166 will help you on how it works. The instruction can be
found in the answer of soegaard :
scheme - Y combinator discussion in “The Little Schemer” - Stack Overflow
When running it with stepper in DrRacket, there are 27 steps for a case (l is (' a b c)), I only demonstrate 4 steps here (press ctrl and + to see the enlarged image)
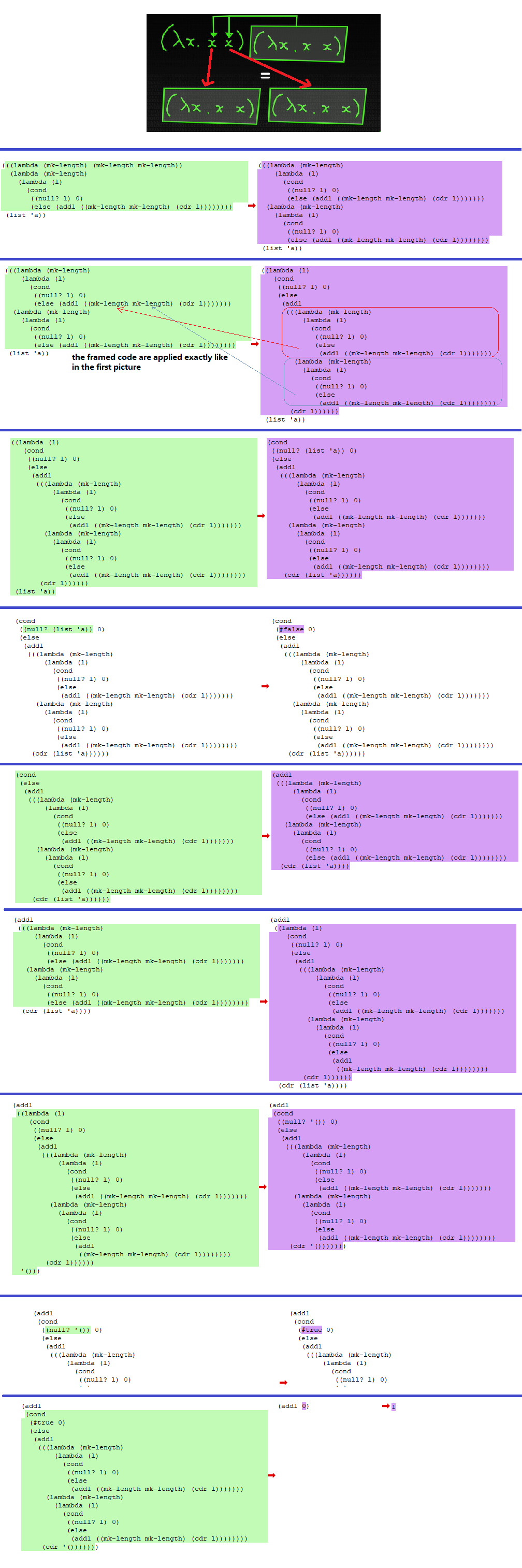
You can try to play with longer list, such as this:
(((lambda (mk-length)
(mk-length mk-length))
(lambda (mk-length)
(lambda (l)
(cond
((null? l) 0 )
(else (add1
((mk-length mk-length)
(cdr l))))))))
'(a b c)) ;<- it works with lists in any length, try itYou would realize that this is just more recurrences of that “bear in mind”
picture, aka calling (mk-length mk-length) one more time before applying a
shorter candidate list, until the (cdr l) runs out of atom. In the end, the null
list becomes the termination condition, without triggering it, we will go stack overflow by calling
(mk-length mk-length) infinite times.
If you find it confusing, read this preview of omega combinator in the first answer of this post:scheme - Y combinator discussion in “The Little Schemer” - Stack Overflow
Let’s further abstract the function with the legitimate though interrupting
(mk-length mk-length) part. Simple, just add another layer, I add some syntax salt (mk-length-two) to distinguish with the original (mk-length i.e. mk-length-one) so you can see it clearer:
((lambda (mk-length)
(mk-length mk-length))
(lambda (mk-length-two)
((lambda (mk-length-one)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (mk-length-one (cdr l)))))))
(lambda (l)
((mk-length-two mk-length-two) l)))))Then we add one last more layer, (I swear it’s the last layer) to switch the order a bit, moving the actual length measuring part to make it look nicer:
((lambda (mk-length-one)
((lambda (mk-length)
(mk-length mk-length))
(lambda (mk-length-two)
(mk-length-one (lambda (l)
((mk-length-two mk-length-two) l))))))
(lambda (mk-length-one)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (mk-length-one (cdr l))))))))That’s very complex, let’s simplify it
((lambda (f)
((lambda (x) (x x))
(lambda (x)
(f (lambda (l)
((x x) l))))))
(lambda (mk-length-one)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (mk-length-one (cdr l))))))))Define and name the first part as Y combinator
(define Y
(lambda (f)
((lambda (x) (x x))
(lambda (x)
(f (lambda (l)
((x x) l)))))))
;and call Y with any function you want
((Y
(lambda (len)
(lambda (l)
(cond
((null? l) 0)
(else (+ 1 (len (cdr l)))))))) '(a b c d))Done. Happy hacking!
Chapter 10 What is the value of all of this?
Firstly this chapter defines entry and table/enviroment. An entry consists of a pair of lists of equal length (length is the number of first level atoms in a list). A list of entries is table/environment.
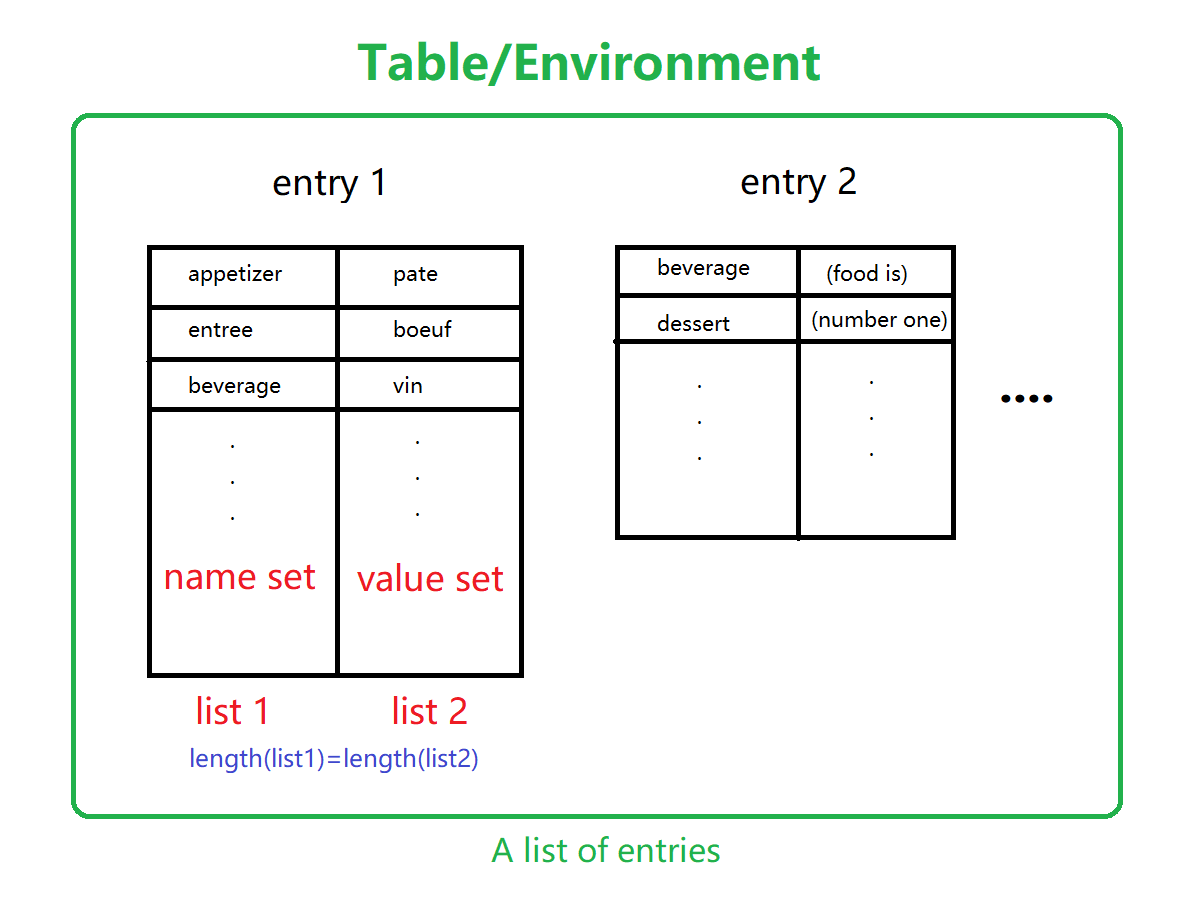
The entries can be built by (cons) lists.
; Let's build entries with build from chapter 7 (07-friends-and-relations.ss)
(define build
(lambda (s1 s2)
(cons s1 (cons s2 '()))))
(define new-entry build)
; Test it out and build the example entries above
(build '(appetizer entree bevarage)
'(pate boeuf vin))We are using entries and tables to write an interpreter in this chapter, which refers to find names with matching values. So in our interested entry, the first list is usually a set of names, and the second list is a set of values corresponding to every names.
Given a function (lookup-in-entry), we would be able to find a value for every
name.
;(lookup-in-entry name entry)
;food --
'((appetizer entree bevarage)
(pate boeuf vin))
(lookup-in-entry entree food)
; -> boeufLet’s try writing it. The (lookup-in-entry) works this way: the (eq?) checks
input with every element in name lists, and return the corresponding value in the
second list. (Remember we always need to return ('()) first if the input is null.)
;(define second
; (lambda (p)
; (car (cdr p))))
;the entry-f take null λ function to make it not break
(define lookup-in-entry
(lambda (name entry entry-f)
(lookup-in-entry-help
name
(first entry)
(second entry)
entry-f)))
; lookup-in-entry uses lookup-in-entry-help helper function
(define lookup-in-entry-help
(lambda (name names values entry-f)
(cond
((null? names) (entry-f name))
((eq? (car names) name) (car values))
(else
(lookup-in-entry-help
name
(cdr names)
(cdr values)
entry-f)))))
; Let's try out lookup-in-entry
(lookup-in-entry
'entree
'((appetizer entree bevarage) (pate boeuf vin))
(lambda (n) '()))
;-> boeuf
; The null function make sure the function doesn't break with incorrect input.
(lookup-in-entry
'no-such-item
'((appetizer entree bevarage) (pate boeuf vin))
(lambda (n) '()))
;-> '()Putting the above code to DrRacket and run with stepper, you can see how things are achieved.
The table/environment can be extended by adding more new pairs (aka entries) on top of the old table/entries.
(define extend-table cons)We can write another (lookup-in-entry) working as above But notice
the take the (car (cdr table)) as input in every recursions, which means the function will immediately cease and return value when the first name matches the input.
; lookup-in-table finds an entry in a table
(define lookup-in-table
(lambda (name table table-f)
(cond
((null? table) (table-f name))
(else
(lookup-in-entry
name
(car table)
(lambda (name)
(lookup-in-table
name
(cdr table)
table-f)))))))
; Let's try lookup-in-table
(lookup-in-table
'beverage
'(((entree dessert) (spaghetti spumoni))
((appetizer entree beverage) (food tastes good)))
(lambda (n) '()))
; -> 'goodThen let’s look at value and type. When asking what’s the value of an S-expression, in most of the cases, it returns the nature of itself. For example, see the value of these S-expression:
(value e) where e is (car (quote (a b c)))
; is a, coz the first element of '(a b c) is an atom
(value e) where e is (quote (car (quote (a b c))))
; is (car (quote (a b c)))
; coz (quote()) make the whole argument literal as a list
; the inner car won't be called.
(value e) where e is
((lambda (nothing)
(cond
(nothing (quote something))
(else (quote nothing))))
#t)
;is something
;coz the e is evaluated first, returned 'something
;'something is an atomWhat is type? Based on the working essence, all the functions we have seen in
this book can be described in six types:
(const, quote, identifier, lambda, cond, application). In interpreting
program, implementing a type classification function in the first step is an
efficiency booster. Because functions in the same type work in similar way. If we can write an universal function for each type, we can call and optimize each function
based on their distinctive characteristics.
The similar part of interpretation is, recognizing the type and arguments of function, finding the
corresponding value for each type and arguments (use (lookup-in-table)), then
implementing the value to the type and arguments.
So firstly let’s how the type classification works. The first layer of
classifier is (expression-to-action) and followed by other more detailed ones.
This is going to be the most important function in this
chapter: it classifies any input into the above six categories
based on the “nature of action” of the input. Then each categories has its own
running/interpreting rules with starred names (e.g. *const, *identifier). With
these starred functions, we can roughly find values for anything, with a proper table.
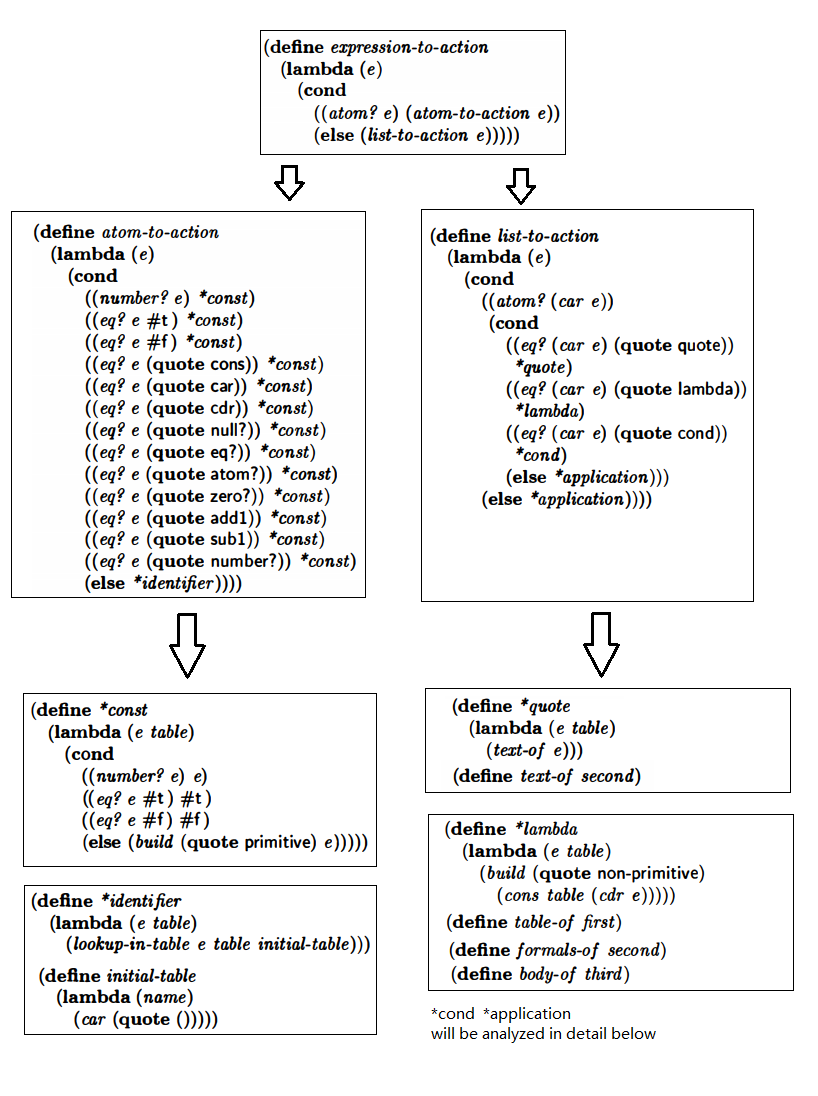
Since everything can be classified with the above function, we can use (meaning e table) to find value for both functions and arguments, and merge the type and value together in a table to further writing implementing
procedure. The above tree code blocks can be linked by two functions as:
; The value function takes an expression and evaulates it
(define value
(lambda (e)
(meaning e '())))
; The meaning function translates an expression to its meaning
(define meaning
(lambda (e table)
((expression-to-action e) e table)))Most of the running rules for the six categories are just writing down details of its working nature. And the examples on book are easy to follow. We will see some difficult ones together: *lambda, *cond, *application.
(1) lambda
We can see that e as an lambda expression, when passed to (meaning e table) it
got classified as *lambda. The following rule of *lambda action defines e as
non-primitive and attaches the table to its remainder. Later we will see in (apply-closure), for a
function defined as non-primitive, we will further deconstruct the content of
itself to run.

(2) cond
The rule for (*cond) category is similar to lambda. As we know an eternal condition of (cond) is
(else) so it’s the first one got translated into meaning. The other predicates
conditions of cond (cond-lines-of e) do not have much varieties either, no much more
than (atom? eq? null? zero? o< o>) with combinations of (and or). These
primitive ones got translated in the second predicate with meaning of (*const)
from the (atom-to-action). The remaining non-usual ones which either goes to atom/identifier or got translated into (*application).
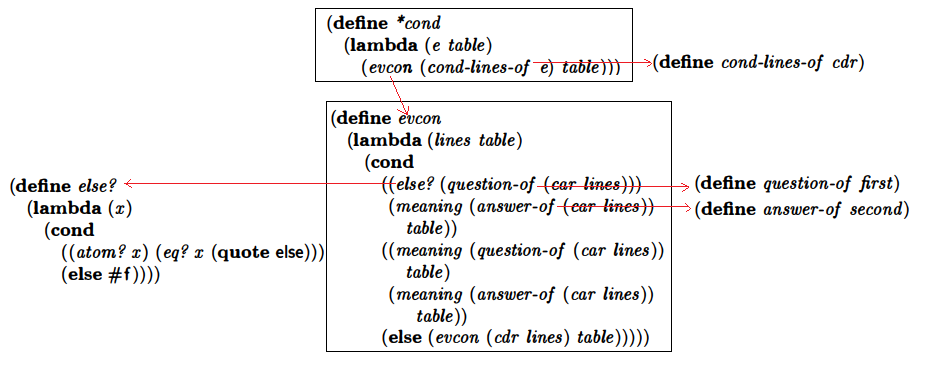
If you wonder, put the book example in DrRacket:
(*cond (cond (coffee klatsch)(else party))
(((coffee)(#t))
((klatsch party)(5 (6)))))And my answer:
The coffee example roughly shows an idea of searching function for meaning/action in
the table when it’s not primitive like (eq?).

(3) application
This category processes all other complex function expressions. For example, a S-expression
applying value to a lambda function.

Starting from a simple example, implementing a lambda expression, is equal to
find the meaning of an e with a table like this:
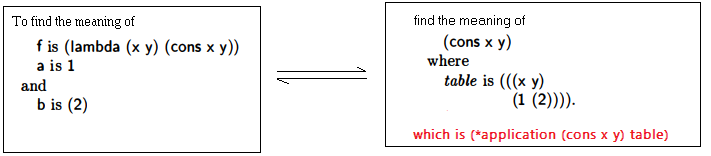
It equals evaluating =(*application (cons x y) table) too. We are not sure what kind of tables will always work, but We would like to have an universal form to do this, maybe with a closure that got functions, arguments and corresponding values stored in a structural form. Evaluating any non-primitive function would be like evaluating the meaning/*application of a standard object.
In fact yes, it is achievable. As is mention in *lambda part, applying a non-primitive function - a closure -
to a list of values is the same as finding the meaning of the closure’s body
with its table extended by an entry of the form (formals values).
In this entry, formals is the formals of the closure and values is the results of evlis.
There may be a thousand possible closures, but let’s start with a simple one
matching a function with known form.
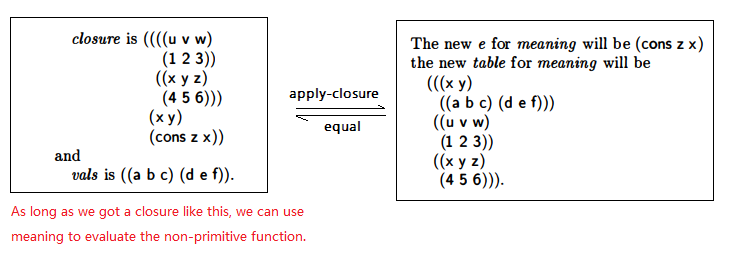
This is how it evolves:

comments powered by Disqus