TOC
Background
Note: the aim of this article is to provide a detailed proof of ANOVA foundation with full notation, not to explain ANOVA. More explaintation can be found in the Youtube link.A
The ANOVA test is to use (rigorous mathmatical based) calculation to infer whether there are differences in performance/data for different groups/treatment. The ANOVA compares the within group variance (SSE:sum of squares within group) and between group variance (SSB: sum of squares between groups). The sum of SSE and SSB happens to equal to the sum of deviation of all the individual observations (SST: total sum of squares). Intuitively speaking with the SST unchanged, if the SSB is very big, the SSE tend to be very small. It’s very likely that these groups are from distinctively different worlds (or population, or distribution) instead of the same world.
Here is an example, compare with the middle sample group, the other two sample
groups are more like from a different population:
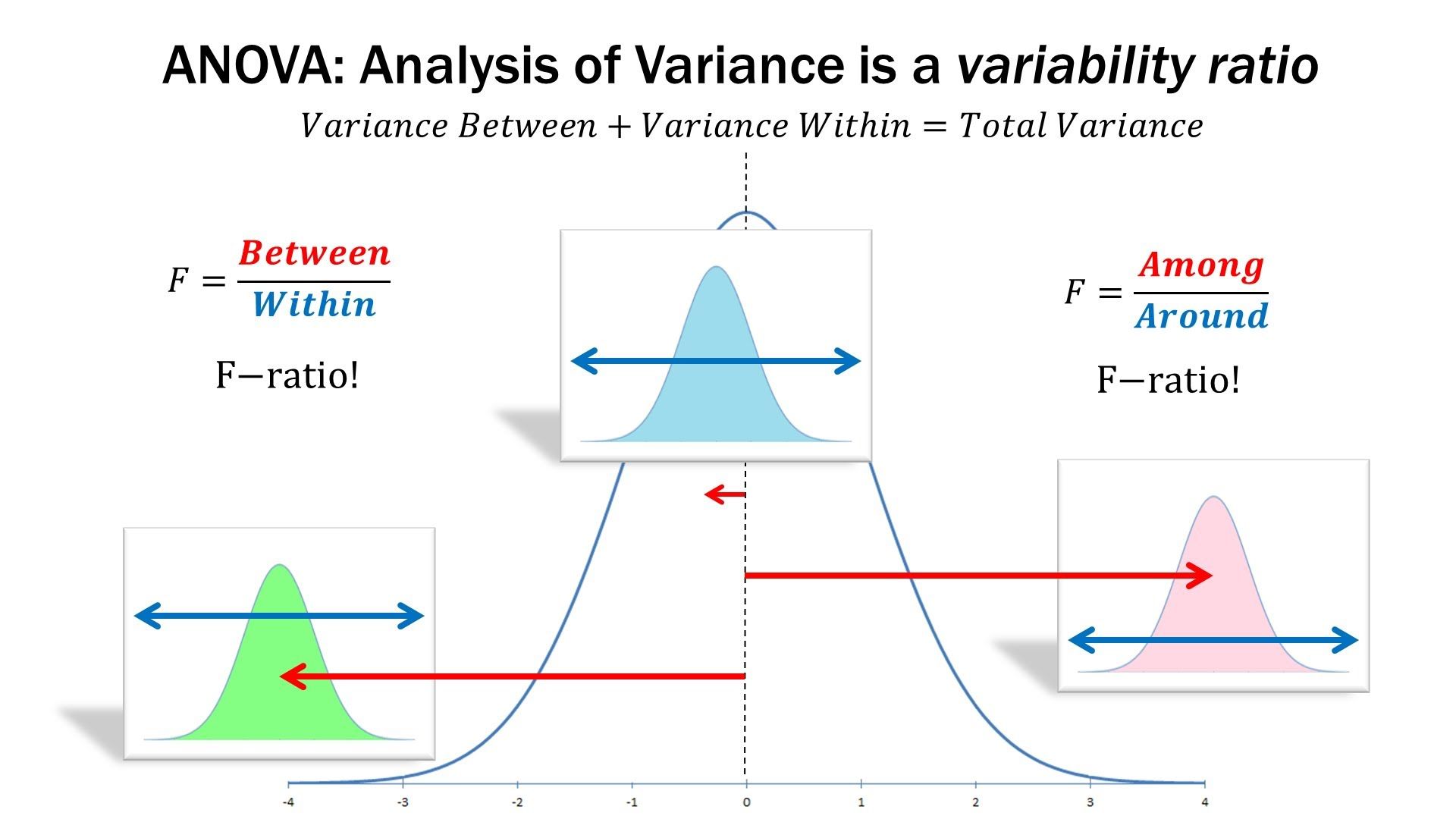Source and detail can be found here: Statistics 101: ANOVA, A Visual Introduction - YouTube
When I review the most foundamental knowledge of ANOVA test, I notice two issues that make me feel necessary to write this detailed proof. (1) The notation is not quite consistent across different materials, especially for non-balanced dataset expression. Non-balanced datasets is that every test group, or treatment has different numbers of observations. This is almost everywhere in real world empirical studies. (2) Some of the prove of SST=SSE+SSB is missing steps or gets too complex in polynomial expansions. The trick of proving multiple summation with polynomials is “not to expand polynomials, but to use more distributive law”.
Notation and Lemma
So here I provide a note with full proof with consistent notations.
SST = SSB + SSE
comments powered by Disqus